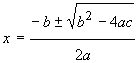Las ecuaciones de segundo grado son de la forma    ax2+ bx + c = 0,  siendo a, b y c números reales (siendo a distinto de cero), donde x recibe el nombre de variable o incógnita, a y b se llaman coeficientes de las incógnitas y c recibe el nombre de término independiente.

    Hemos exigido que a sea no nulo, ya que en caso de serlo, tendríamos una ecuación de primer grado.

 

 

Clasificación. 

                     Las ecuaciones de segundo grado se van a clasificar en: 

1. Completas:   

     Si son de la forma: ax2+bx+c=0, siendo a, b y c números reales distintos de cero.

1. Incompletas:  

    Distinguiendo dos casos:

1. • < >Si b = 0, quedando la ecuación  ax2 + c = 0

     Si el término independiente c = 0, quedando la ecuación  ax2 + bx = 0

   • Si b=0 y c=0, quedando la ecuación ax2 =  0

 

 

Número de soluciones reales. Discriminante.  

    La ecuación de segundo grado:   ax2+bx+c=0   puede tener una, dos o ninguna solución Para averiguarlo sin tener que resolver la ecuación vamos a recurrir al discriminante de una ecuación de segundo grado. El valor del discriminante (al que vamos a llamar  D)  viene dado por  D = b2 - 4ac

            Si  D > 0 ,  la ecuación tiene dos soluciones reales distintas.

               Si  D = 0 ,  la ecuación tiene dos soluciones reales iguales  (Una solución doble). 

            Si  D < 0 ,  la ecuación no tiene solución real.

 

Resolución.  

La siguiente expresión o fórmula, nos permite hallar las raíces o soluciones de la ecuación de segundo grado. 

 

 

   

 

 

 

 

 

 

Para ello, basta con identificar los coeficientes a, b y c de la ecuación , sustituir sus valores en  dicha fórmula y hacer las operaciones indicadas.

    A continuación, veamos cómo se obtiene dicha fórmula en 7 pasos:

                        

Sea la ecuación de segundo grado  ax2+bx+c=0.

 

1º, asilamos el término independiente                     ax2+bx = - c

 

2º, multiplicamos ambos miembros por 4a:            4a2x2+4abx = - 4ac

 

3º, sumamos b2 en ambos miembros:                      4a2x2+4abx + b2 = - 4ac + b2

 

4º, considerando las identidades notables               (2ax+b)2 = - 4ac + b2 

 

5º, extraemos la raíz cuadrada                                

6º, pasamos b al segundo miembro                          

 

7º, despejamos x                                                      

    La expresión que acabamos de ver, permite resolver cualquier ecuación de segundo grado. Sin embargo, las ecuaciones de segundo grado incompletas, se pueden resolver de forma más sencilla todavía, sin necesidad de utilizar dicha expresión:

​

• Las ecuaciones incompletas, del tipo  ax2+bx= 0, se resuelven sacando factor común x, e igualando los dos factores  a cero, esto es:

Sea la ecuación de segundo grado incompleta  ax2+bx=0
 

 

• Las ecuaciones incompletas, del tipo  ax2+c = 0, se resuelven despejando x2, y posteriormente para obtener x, considerar la solución positiva y la negativa de la raíz cuadrada, esto es:

 

Sea la ecuación de segundo grado  incompleta  ax2+c=0.